什么是开方？

什么是开方？

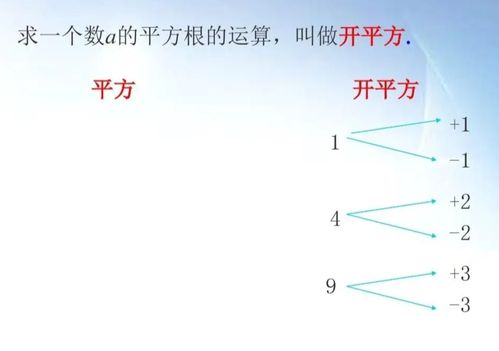
在数学中，开方是一个基本的运算，它指的是求一个数的方根的过程。方根，简单来说，就是一个数乘以自己几次可以得到原数的结果。例如，4的平方根是2，因为2乘以2等于4。开方是乘方的逆运算，即如果我们知道一个数的平方是另一个数，那么开方就是找出这个数的过程。

开方的理解

为了更好地理解开方，我们可以通过一些具体的例子来说明。比如，我们知道2的平方是4，即2乘以2等于4；同样，3的平方是9，即3乘以3等于9。如果我们想要找出4的平方根，我们实际上是在寻找一个数，这个数乘以自己等于4。显然，这个数就是2，因为2乘以2等于4。同理，9的平方根是3，因为3乘以3等于9。

开方的符号和表示

在数学表达式中，开方通常用根号符号“√”来表示。例如，√4表示求4的平方根。如果我们要表示求一个数的n次方根，我们可以在根号符号的右上角写上n，如√(4^2)表示求4的平方根，也就是2。在更复杂的数学表达式中，开方还可以用于表示更高级的数学概念，如复数的开方等。

开方在数学中的应用

开方在数学中有着广泛的应用。在几何学中，开方可以帮助我们计算图形的面积和体积。例如，计算一个正方形的面积时，我们只需要知道它的边长，然后将其平方即可得到面积。在代数中，开方是解方程和不等式的重要工具。例如，解方程x^2=4时，我们可以通过开方得到x=±2，因为2乘以2等于4，而-2乘以-2也等于4。

开方在现实生活中的应用

开方不仅在数学领域有着重要的应用，在现实生活中也有着广泛的应用。例如，在建筑行业中，开方可以帮助工程师计算材料的面积和体积；在物理学中，开方可以用于计算速度、加速度等物理量的平方根；在经济学中，开方可以用于计算利率、投资回报率等。

开方的计算方法

开方的计算方法有很多种，包括直接计算、使用计算器、以及通过近似方法计算。对于简单的开方，如√4，我们可以直接得出答案2。对于更复杂的开方，如√17，我们可以使用计算器来得到精确的结果。在缺乏计算器的情况下，我们可以使用近似方法，如牛顿迭代法，来逼近开方的结果。

开方的性质和规则

开方有一些基本的性质和规则，这些性质和规则对于理解和应用开方非常重要。例如，任何正数的平方根都是正数，而0的平方根是0。另外，负数没有实数平方根，因为任何实数的平方都是非负的。开方还有一个重要的规则，即根号内的乘法可以分解为根号外的乘法，如√(ab)=√a√b，只要a和b都是非负数。

开方是数学中的一个基本运算，它不仅有着丰富的理论内涵，而且在现实生活中的应用也非常广泛。通过理解开方的定义、计算方法、性质和规则，我们可以更好地掌握这一数学工具，并在各个领域中发挥其作用。

推荐您阅读更多有关于“ ”的文章

猜你喜欢